احصل على معلومات المنتج بسرعة في دقيقة واحدة
نظام مرجعي للوضع والاتجاهيُعدّ نظام تحديد الاتجاه والوضع (AHRS) جهازًا ملاحيًا أساسيًا يستخدم دمج بيانات من عدة مستشعرات لحساب الوضع ثلاثي الأبعاد (زاوية الميل، زاوية الدوران) وزاوية الاتجاه لحاملة الطائرات في الوقت الفعلي. تشمل تقنياته الأساسية مجالات مثل الأنظمة الكهروميكانيكية الدقيقة (MEMS)، والملاحة بالقصور الذاتي، ومعالجة الإشارات، والتحسين غير الخطي. ستتناول هذه المقالة الجوانب التقنية من ثلاثة أبعاد: النماذج الرياضية، وتنفيذ الخوارزميات، وتعويض الأخطاء.
إن المبدأ الأساسي لنظام AHRS هو دمج البيانات من أجهزة استشعار متعددة، مما يعوض عن قيود جهاز استشعار واحد من خلال أجهزة استشعار تكميلية.
أ. الجيروسكوب: يقيس السرعة الزاوية باستخدام تأثير كوريوليس ويكاملها للحصول على تغييرات في الوضع، ولكن لا يوجد انحراف انحياز (خطأ متراكم بمرور الوقت).
ب. مقياس التسارع: يقيس القوة المحددة (التسارع الجاذبي + تسارع الحركة) ويمكن استخدامه لمعايرة الوضع (الدوران، الميل) عند السرعة الثابتة أو الثابتة.
ج. مقياس المغناطيسية: يقيس اتجاه المجال المغناطيسي الأرضي، ويوفر اتجاهًا مطلقًا (زاوية الانحراف)، ولكنه عرضة للتداخل المغناطيسي الصلب/اللين.
د. نظام تحديد المواقع العالمي (GPS) الاختياري: يساعد في تصحيح أخطاء الموقع والسرعة.
المعادلة التفاضلية لتحديث السرعة الزاوية للحاملة ووضعها:
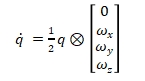
فيما بينها،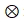 
يمثل ضرب الكواترنيون و 
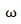هي السرعة الزاوية التي يقيسها الجيروسكوب (بالراديان/ثانية)
يكمن التحدي الأساسي لنظام تحديد الاتجاه والحركة (AHRS) في كيفية دمج البيانات من الجيروسكوبات (ذات الاستجابة الديناميكية الممتازة ولكنها تعاني من الانحراف)، ومقاييس التسارع (ذات الدقة الثابتة العالية ولكنها عرضة لتداخل الحركة)، ومقاييس المغناطيسية (التي توفر الاتجاه المطلق ولكنها عرضة للتداخل). وفيما يلي الخوارزميات الرئيسية المستخدمة:
استنادًا إلى نموذج فضاء الحالة، يتم تقدير الوضع بشكل متكرر من خلال التنبؤ (تكامل الجيروسكوب) والتحديث (ملاحظة مقياس التسارع / مقياس المغناطيسية).
يتم بناء متجه الحالة على النحو التالي، بما في ذلك زاوية خطأ الاتجاه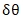 
وانحياز الجيروسكوب 
.
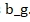تُستخدم قيم الباقي من متجه الجاذبية المقاس بواسطة مقياس التسارع والمجال المغناطيسي الأرضي المقاس بواسطة مقياس المغناطيسية كقيم للملاحظة، ويتم بناء معادلة الملاحظة التالية:
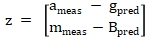
في ضبط التغاير، تغاير الضوضاء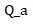 
عادةً ما يتم ضبط مقياس التسارع على 
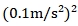وتغاير الضوضاء 
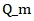تم ضبط مقياس المغناطيسية على 
.
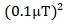دمج مُرجّح لبيانات الجيروسكوب عالية التردد وبيانات مقياس التسارع/المغناطيسية منخفضة التردد. ميزته انخفاض الحمل الحسابي وملاءمته للأنظمة المدمجة؛ أما عيبه فهو اعتماد ضبط المعلمات على الخبرة ومحدودية الأداء الديناميكي.
يستخدم الجزء عالي التردد تكامل الجيروسكوب، بينما يستخدم الجزء منخفض التردد معايرة باستخدام مقاييس التسارع/المغناطيسية:
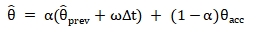
ثابت الزمن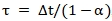 
يستغرق الأمر عادةً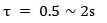 
توجد خوارزميتان رئيسيتان لتحسين التدرج الهبوطي. تعتمد خوارزمية ماهوني على الترشيح التكميلي غير الخطي الرباعي وتصحح انحياز الجيروسكوب من خلال وحدة تحكم تناسبية تكاملية؛ أما خوارزمية مادجويك فتُحسّن الرباعيات مباشرةً عن طريق تقليل دالة الخطأ بين قياسات المستشعر والتنبؤات، مما ينتج عنه كفاءة حسابية عالية وملاءمة لسيناريوهات الطاقة المنخفضة.
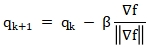
فيما بينها،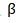 
وهو عامل معدل التقارب، وتتراوح قيمه النموذجية من 0.1 إلى 0.5.
يجب تقدير الانحياز الصفري للجيروسكوب وتعويضه عبر الإنترنت (مثل من خلال تهيئة الحالة الثابتة)؛ يمكن أن يؤدي تسارع الحركة إلى تعطيل قياس اتجاه الجاذبية، لذلك، يجب اكتشاف التداخل الديناميكي من مقاييس التسارع من خلال الترشيح عالي التمرير أو اكتشاف حالة الحركة؛
يجب تصحيح تأثير تغيرات درجة الحرارة على الجيروسكوبات ومقاييس التسارع من خلال إنشاء نموذج تعويض درجة الحرارة؛
يتطلب تداخل مقياس المغناطيسية معايرة مغناطيسية صلبة/لينة (تركيب القطع الناقص أو خوارزمية تعتمد على مجال المعايرة).
يؤدي الاهتزاز عالي التردد إلى زيادة ضوضاء مقياس التسارع، مما يستدعي عزله ميكانيكيًا أو ترشيحه رقميًا. عند القيام بمناورات سريعة (مثل دوران الطائرة بدون طيار)، يتعطل مقياس التسارع، ويحتاج الجيروسكوب النقي إلى العمل لفترة وجيزة.
تتطلب السيناريوهات الديناميكية العالية خوارزميات لإكمال التكرارات في أجزاء من الثانية (مثل دورات التحكم في الطائرات بدون طيار).<10 مللي ثانية). تتطلب المنصات المدمجة مثل STM32 تحسين عمليات الفاصلة العائمة أو اعتماد معالجة الأرقام ذات الفاصلة الثابتة.
يتطلب جمع بيانات المستشعرات تزامنًا زمنيًا دقيقًا، وإلا سيزداد خطأ الدمج. يجب تعويض تأخير الإرسال في واجهات الاتصال (مثل SPI/I2C).
يحتاج النظام إلى التقارب بسرعة أثناء بدء التشغيل (مثل تهيئة مقياس التسارع/مقياس المغناطيسية في حالة ثابتة). ويتطلب تصميم النظام تصميمًا قويًا لمقاومة القيم الشاذة (مثل التداخل اللحظي من مقاييس المغناطيسية).
أ. دمج البيانات بمساعدة التعلم العميق: استخدام الشبكات العصبية لنمذجة الأخطاء المعقدة والخصائص غير الخطية.
ب.تحسين دمج المصادر المتعددة: الجمع بين الرؤية (VIO) أو نظام الملاحة العالمي عبر الأقمار الصناعية (GNSS) أو مقياس الضغط الجوي لتحسين الموثوقية في البيئات المعقدة.
ج.التقدم في تكنولوجيا الأنظمة الكهروميكانيكية الدقيقة: ستؤدي الجيروسكوبات ذات الدقة العالية والضوضاء المنخفضة (مثل الجيروسكوبات البصرية الكهروميكانيكية الدقيقة) إلى تقليل عبء الخوارزمية.
د.تحسين الحوسبة الطرفية: خوارزمية خفيفة الوزن لرقائق الذكاء الاصطناعي المدمجة (مثل ARM Cortex-M7).
يمثل التطور التكنولوجي لأنظمة الملاحة الآلية المتقدمة (AHRS) تداخلاً عميقاً بين الرياضيات والفيزياء والهندسة. فمن الحل الفوري للمعادلات التفاضلية الرباعية إلى كبح الضوضاء في مستشعرات الأنظمة الكهروميكانيكية الدقيقة (MEMS)، يؤثر كل تفصيل تقني بشكل مباشر على الأداء النهائي للنظام. ومع تحسن قدرة الحوسبة الطرفية وجدوى... أجهزة استشعار عالية الدقةالجيل القادم من نظام AHRS سيحقق ذلك إدراكًا للاهتزاز الزاوي على مستوى النانومتر وقدرة كاملة على مقاومة التداخل، مما يمنح الأنظمة غير المأهولة دقة إدراكية فضائية تتجاوز قدرة البشر.
Xml سياسة الخصوصية المدونة خريطة الموقع
حقوق النشر
@ شركة مايكرو ماجيك كل الحقوق محفوظة.
دعم الشبكة
بالعربية
